Skip to main content

CHAPTER 5 – Time Value of Money 2

Questions

5-1 How can you add a cash flow in year two and a cash flow in year four in year seven?


To add cash flows, they need to be moved to the same time period. The cash flows in years two and four should be moved forward with interest to year seven, then they can be added together.


5-2 People can become millionaires in their retirement years quite easily if they start saving early in employer 401(k) or 403(b) programs (or even if their employers don’t offer such programs). Demonstrate the growth of a $250 monthly contribution for 40 years earning 9 percent APR.


Using equation 5-2, we have:


5-3 When you discount multiple cash flows, how does the future period that a cash flow is paid affect its present value and its contribution to the value of all the cash flows?


Discounting reduces a future cash flow to a smaller present value. Cash flows far into the future become very small when discounted to the present. Thus, cash flows in distant future periods have small impacts on present values.


5-4 How can you use the present value of an annuity concept to determine the price of a house you can afford?


Mortgages are typically for a large enough amount of money that borrowing is required to purchase a home. The amount that one can afford for a home is a function of their current state of wealth. Mortgages allow consumers to spread the expense of a home over a longer period, typically 15 or 30 years. This allows consumers to put a smaller portion of wealth into the home (for example, a 20% down payment) and borrow the balance over the life of the loan. Due to the effect of annuity compounding, the payments for such a long lived debt make the monthly payments of a manageable nature so that they can be paid from current income.


5-5 Since perpetuity payments continue for ever, how can a present value be computed? Why isn’t the present value infinite?


Equation 5-5 is used to calculate the present value of a perpetuity. It is a limiting version of equation 5-4 in which the period N grows infinitely large. As this occurs the expression following the “1” in equation 5-4 drives to the value 0 and the numerator simply become “1.” The present value is not infinite since the terms following the PMT in equation 5-4 converge to a finite limit of 1/i. This also demonstrates how payments far into the future have infinitesimal value today.


5-6 Explain why you use the same adjustment factor, (1 + i), when you adjust annuity due payments for both future value and present value.


Adjusting an annuity due calculation involves shifting the entire series of payments forward one period. This is accomplished by multiplying by (1 + i) irrespective of whether it is a future value or present value calculation.


5-7 Use the idea of compound interest to explain why EAR is larger than APR.


The annual percentage rate does not take into account the frequency of interest compounding. Equation 5-8 illustrates the conversion from APR to EAR. The effective annual rate converts the annual percentage rate to a rate that can be compared to other annual rates.


5-8 Would you rather pay $10,000 for a five year $2,500 annuity or a ten-year $1,250 annuity? Why?


The effective annual rates for these two payment streams are 7.93% and 4.28% respectively. I would rather pay $10,000 for a five year $2,500 annuity as it earns a higher effective annual rate of interest.


5-9 The interest on your home mortgage is tax deductible. Why are the early years of the mortgage more helpful in reducing taxes than in the later years?


Mortgage payments at the beginning of the amortization schedule are predominantly interest with little principal. In later years, interest payments decline and principal payments make up an ever increasing part of the payments. Thus, the tax deductible part (the interest payment) is larger in the beginning years.


5-10 How can you use the concepts illustrated in computing the number of payments in an annuity to figure how to pay off a credit card balance? How does the magnitude of the payment impact the number of months?


Utilizing equation 5-2, you can declare the present balance for the credit card and set that equal to the PVA. The interest can be obtained as an APR and converted to and EAR using equation 5-8. This is the value to put into “i” in equation 5-2. You then decide when you want to have the credit card paid off and convert this to a monthly value of N in equation 5-2. Solving for PMT will yield the amount needed to pay the credit card off in the time frame you desire, assuming that no additional charges are made to the credit card and that the interest rate remains level.


Problems

5-1 Future Value Compute the future value in year 8 of a $1,000 deposit in year 1 and another $1,500 deposit at the end of year 3 using a 10% interest rate.


Use equation 5-1:

FV = $1,000 × (1 + 0.10)7 + $1,500× (1 + 0.10)5 = $1,948.72 + $2,415.77 = $4,364.48


5-2 Future Value Compute the future value in year 7 of a $2,000 deposit in year 1 and another $2,500 deposit at the end of year 4 using a 8% interest rate.


Use equation 5-1:

FV = $2,000 × (1 + 0.08)6 + $2,500 × (1 + 0.08)3 = $3,173.75 + $3,149.28 = $6,323.03


5-3 Future Value of an Annuity What is the future value of a $500 annuity payment over 5 years if interest rates are 9 percent?


Use equation 5-2:

5-4 Future Value of an Annuity What is the future value of a $700 annuity payment over 4 years if interest rates are 10 percent?


Use equation 5-2:



5-5 Present Value Compute the present value of a $1,000 deposit in year 1 and another $1,500 deposit at the end of year 3 if interest rates are 10 percent.


Use equation 5-3:


PV = $1,000 ÷ (1 + 0.10)1 + $1,500 ÷ (1 + 0.10)3 = $909.09 + $1,126.97 = $2,036.06


5-6 Present Value Compute the present value of a $2,000 deposit in year 1 and another $2,500 deposit at the end of year 4 using an 8% interest rate.


Use equation 5-3:

PV = $2,000 ÷ (1 + 0.08)1 + $2,500 ÷ (1 + 0.08)4 = $1,851.85 + $1,837.57 = $3,689.43


5-7 Present Value of an Annuity What’s the present value of a $500 annuity payment over 5 years if interest rates are 9 percent?


Use equation 5-4:

5-8 Present Value of an Annuity What’s the present value of a $700 annuity payment over 4 years if interest rates are 10 percent?


Use equation 5-4:




5-9 Present Value of a Perpetuity What’s the present value, when interest rates are 7.5 percent, of a $50 payment made every year forever?


Use equation 5-5:




5-10 Present Value of a Perpetuity What’s the present value, when interest rates are 8.5 percent, of a $75 payment made every year forever?


Use equation 5-5:




Labels:

Comments

  1. AdyOctober 2, 2020 at 4:07 AM

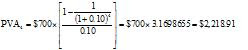
    Nice work this blog gives clear knowledge about investment. stockinvestor.in is a stock related website which provides all stock market information.
    Sensex
    buy and sell
    shares
    stock exchanges

    ReplyDelete

Post a Comment

Popular posts from this blog

CHAPTER 8 – UNDERSTANDING FINANCIAL MARKETS AND INSTITUTIONS

Questions 1. Classify the following transactions as taking place in the primary or secondary markets: a. IBM issues $200 million of new common stock – primary market b. The New Company issues $50 million of common stock in an IPO – primary market c. IBM sells $5 million of GM preferred stock out of its marketable securities portfolio – secondary market d. The Magellan Fund buys $100 million of previously issued IBM bonds – secondary market e. Prudential Insurance Co. sells $10 million of GM common stock – secondary market 2. Classify the following financial instruments as money market securities or capital market securities: a. Federal Funds – money market security b. Common Stock – capital market security c. Corporate Bonds – capital market security d. Mortgages – capital market security e. Negotiable Certificates of Deposit – money market security f. U.S. Treasur...
16 comments
Read more

CHAPTER 6 – Valuing Bonds

CHAPTER 6 – Valuing Bonds Questions 1. What does a call provision allow the issuer to do, and why would they do it? A call provision on a bond issue allows the issuer to pay off the bond debt early at a cost of the principal plus any call premium. Most of the time a bond issuer is called, it is because interest rates have substantially declined in the economy. The issuer calls the existing bonds and issues new bonds at the lower interest rate. This reduces the interest payments the issuer must pay each year. 2. List the differences between the new TIPS and traditional Treasury bonds. Traditional Treasury bonds have a fixed principal and constant payments. Because the principal and coupon rate are fixed, interest rate changes in the economy cause the market price of the bonds to have large fluctuations. On the other hand, the principal of a TIPS increases with the rate of inflation. Similar to a T-bond, the TIPS has a constant coupon rate. However, since the principal of the TIP...
10 comments
Read more

CHAPTER 2 – REVIEWING FINANCIAL STATEMENTS

1. List and describe the four major financial statements. The four basic financial statements are: 1. The balance sheet reports a firm’s assets, liabilities, and equity at a particular point in time. 2. The income statement shows the total revenues that a firm earns and the total expenses the firm incurs to generate those revenues over a specific period of time—generally one year. 3. The statement of cash flows shows the firm’s cash flows over a given period of time. This statement reports the amounts of cash that the firm generated and distributed during a particular time period. The bottom line on the statement of cash flows―the difference between cash sources and uses―equals the change in cash on the firm’s balance sheet from the previous year’s cash account balance. 4. The statement of retained earnings provides additional details about changes in retained earnings during a reporting period. This financial statement reconciles net income earned during a given period and any cas...
4 comments
Read more